Lesson 11: lambda, map

ref

https://guebin.github.io/DV2022/posts/2022-10-12-6wk-12.html

imports

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

lambda, map (\(\star\))

lambda

- 예제1: 람다표현식(lambda expression)자체가 하나의 오브젝트임

lambda x: (x-2)**2 ### lambda x: (x-2)**2 가 실행되는 순간 메모리상에 함수 오브젝트가 저장됨 

<function __main__.<lambda>(x)>

• “lambda x: (x-2)**2” 는 \(lambda(x)=(x-2)^2\)의 느낌으로 기억하면 쉬움

(사용방법)

(lambda x: (x-2)**2)(2) # 입력2 -> 출력 (2-2)^2 =0 

0

(lambda x: (x-2)**2)(5) # 입력5 -> 출력 (5-2)^2 =9

9

(lambda x: (x-2)**2)(6) # 입력6 -> 출력 (6-2)^2 =16

16

(lambda x: (x-2)**2)(-2) # 입력-2 -> 출력 (-2-2)^2 =16

16

Quiz

\(f(x)=\sqrt{x}\) 를 수행하는 함수를 lambda를 이용하여 구성하라.

- 예제2: 람다표현식에 이름을 줄 수 있음.

f = lambda x: (x-2)**2

f(2),f(4),f(6),f(-2)

(0, 4, 16, 16)

위의 코드는 아래와 같다.

def f(x):
    return (x-2)**2
f(2),f(4),f(6),f(-2)

(0, 4, 16, 16)

- 예제3: 조건부 출력

f = lambda x,y: x if x>y else y # x,y가 입력 -> x>y 일때만 x를 리턴하고 그렇지않으면 y를 리턴 = 큰값을 리턴하라는 소리임 

f(1,20)

20

Quiz

임의의 알파벳 문자열을 입력으로 하고, 알파벳이 대문자이면 “대문자 입니다”를 출력하고 소문자이면 “소문자 입니다”를 출력하는 함수를 구성하라.

(힌트) 아래코드 이용

'a'.isupper()

False

- 예제4: 람다표현식들의 리스트

fl = [lambda x: x, lambda x: x**2, lambda x: x**3]

for f in fl: 
    print(f(2))

2
4
8

x = np.linspace(-1,1,100)
for f in fl:
    plt.plot(x,f(x),'--') 

- 예제5: 람다표현식들의 딕셔너리

fd = {'f1':lambda x: x, 'f2':lambda x: x**2, 'f3':lambda x: x**3}
fd

{'f1': <function __main__.<lambda>(x)>,
 'f2': <function __main__.<lambda>(x)>,
 'f3': <function __main__.<lambda>(x)>}

for k in fd:
    plt.plot(x,fd[k](x),'--')

- 예제6: 람다표현식을 리턴하는 함수 (함수를 리턴하는 함수)

(예비학습) 함수 \(g(x)\)가 정의되어 있을때 \(\frac{d}{dx}g(x)\)의 값을 계산해보기

g = lambda x: x**2 

gg = lambda x : (g(x+0.001)-g(x))/0.001

gg(4)

8.0010000000037

(목표) 도함수를 구해주는 derivate 함수를 정의하자. 이 함수는 임의의 함수 g를 입력으로 받으면, g의 도함수(gg)가 리턴되는 기능을 가진다.

def derivate(g):
    return lambda x : (g(x+0.001)-g(x))/0.001

(사용1)

gg = derivate(g) 

x = np.linspace(0,6.28,1000) 

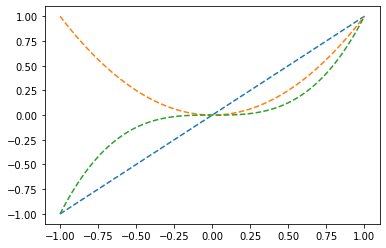
plt.plot(x,g(x),label=r'$f(x)=sin(x)$')
plt.plot(x,gg(x),label=r'$\frac{d}{dx}f(x)=cos(x)$')
plt.legend(fontsize=15)

<matplotlib.legend.Legend at 0x7fa54cde3a50>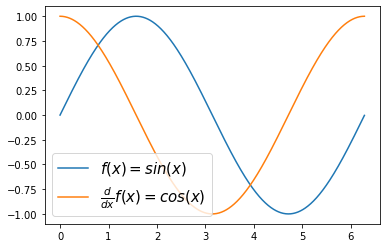

(사용2)

g0 = lambda x: (1/6)*x**3
g1 = derivate(g0) # (1/2)x^2 
g2 = derivate(g1) # x 

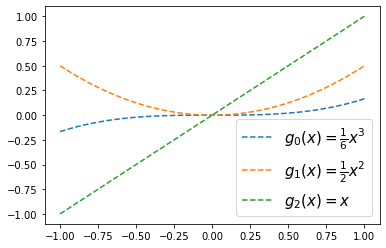
x = np.linspace(-1,1,100)
plt.plot(x,g0(x),'--',label=r'$g_0(x)=\frac{1}{6}x^3$')
plt.plot(x,g1(x),'--',label=r'$g_1(x)=\frac{1}{2}x^2$')
plt.plot(x,g2(x),'--',label=r'$g_2(x)=x$')
plt.legend(fontsize=15)

<matplotlib.legend.Legend at 0x7f662b86ed10>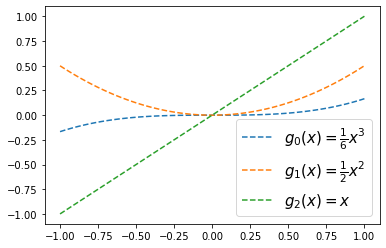

- 예제7: 예제6의 다른표현

derivate = lambda g: lambda x : (g(x+0.001)-g(x))/0.001

(사용1)

g = lambda x: np.sin(x) 

gg = derivate(g) 

x = np.linspace(0,6.28,1000) 

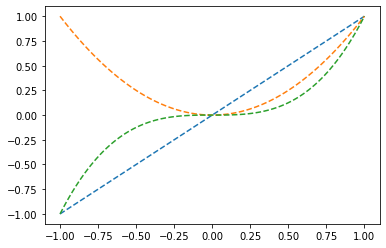
plt.plot(x,g(x),label=r'$f(x)=sin(x)$')
plt.plot(x,gg(x),label=r'$\frac{d}{dx}f(x)=cos(x)$')
plt.legend(fontsize=15)

<matplotlib.legend.Legend at 0x7f662b5fef50>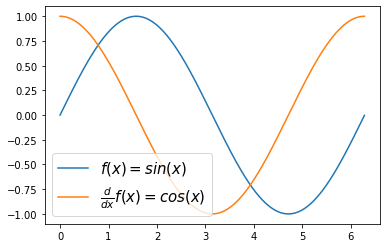

(사용2)

g0 = lambda x: (1/6)*x**3
g1 = derivate(g0) # (1/2)x^2 
g2 = derivate(g1) # x 

x = np.linspace(-1,1,100)
plt.plot(x,g0(x),'--',label=r'$g_0(x)=\frac{1}{6}x^3$')
plt.plot(x,g1(x),'--',label=r'$g_1(x)=\frac{1}{2}x^2$')
plt.plot(x,g2(x),'--',label=r'$g_2(x)=x$')
plt.legend(fontsize=15)

<matplotlib.legend.Legend at 0x7f662b4e78d0>

map

- 개념: $(f,[x_1,x_2,,x_n] )=$

- 예제1:

x = [1,2,3] 
f = lambda x: x+1 
y = list(map(f,x))

(다른구현1)

list(map(lambda x: x+1,[1,2,3]))

[2, 3, 4]

(다른구현2)

f = lambda x: x+1 
[f(xi) for xi in [1,2,3]]

[2, 3, 4]

(다른구현3)

[(lambda x: x+1)(xi) for xi in [1,2,3]]

[2, 3, 4]

(다른구현4)–최악

y = [] 
x = [1,2,3] 
f = lambda x: x+1 
for xi in x:
    y.append(f(xi))

y

[2, 3, 4]

(다른구현5)–더 최악

y = [] 
x = [1,2,3] 
f = lambda x: x+1 
for i in range(len(x)):
    y.append(f(x[i]))

y

[2, 3, 4]

Quiz

\(x=[1,2,3,4,5]\)에 대하여 \(x^2\)을 수행하는 함수를 구현하라.

- 예제2: 문자열을 입력으로 받고 대문자이면 True, 소문자이면 False

입력: A,B,C,a,b,c
출력: T,T,T,F,F,F

x= list('ABCabc')
# x = ['A','B','C','a','b','c']
f = lambda s: s.isupper()
y = list(map(f,x))

x,y

(['A', 'B', 'C', 'a', 'b', 'c'], [True, True, True, False, False, False])

- 예제3: 두개의 입력을 받는 함수 (map을 이용하는 것이 리스트 컴프리헨션보다 조금 편한것 같다)

list(map(lambda x,y: x+y, [1,2,3],[-1,-2,-3]))

[0, 0, 0]

(다른구현)– 리스트컴프리헨션

f = lambda x,y: x+y 
[f(x,y) for x,y in zip([1,2,3],[-1,-2,-3])] 

[0, 0, 0]

quiz

t=np.linspace(-3.14,3.14,100)
x=np.sin(t)
y=np.cos(t)

plt.plot(t,x)
plt.plot(t,y)

\(f(x,y) = max(x,y)\) 를 구현하여 \({\bf x}\),\({\bf y}\) 각 원소에 적용하고 결과를 시각화 하라.

f = (lambda x,y: max(x,y))
f(3,4)

4

z= list(map(f,x,y))

plt.plot(t,z)

- 예제4: map은 “하나의 함수에 다양한 입력”을 적용하는 경우에만 사용가능, 리스트컴프리헨션은 “다양한 함수에 다양한 입력” 지원

flst = [lambda x: x+1, lambda x: x+2, lambda x:x+3] 

map으로 구현시도 \(\to\) 실패

list(map(flst,[-1,-2,-3])) # 결과가 0,0,0

TypeError: 'list' object is not callable

리스트컴프리헨션으로 구현시도 \(\to\) 성공

[f(x) for f,x in zip(flst,[-1,-2,-3])]

[0, 0, 0]

- 종합: map과 리스트컴프리헨션과 비교

• map은 for문을 위한 \(i\)등의 인덱스를 쓰지 않지만 리스트컴프리헨션은 필요함
• map은 좀더 리스트컴프리헨션보다 제약적으로 사용할 수 밖에 없음.

Quiz

1.

아래와 같은 수열이 있다고 하자.

x=np.random.randint(low=0,high=5,size=100)
x

array([1, 1, 4, 0, 2, 3, 2, 1, 4, 4, 0, 0, 3, 0, 1, 3, 1, 0, 0, 1, 2, 1,
       1, 0, 0, 1, 2, 1, 2, 0, 0, 1, 3, 4, 0, 0, 3, 0, 0, 0, 3, 4, 3, 4,
       0, 3, 0, 0, 4, 0, 4, 0, 3, 3, 4, 0, 4, 2, 0, 1, 1, 1, 3, 0, 1, 1,
       4, 1, 1, 4, 1, 0, 4, 2, 1, 2, 0, 0, 1, 3, 3, 2, 0, 3, 3, 3, 0, 4,
       2, 1, 3, 0, 2, 3, 0, 3, 4, 2, 1, 3])

\({\tt x}\)의 각 원소에 아래와 같은 변환을 수행하라.

• 0 \(\to\) ‘사과’
• 1 \(\to\) ‘배’
• 2 \(\to\) ‘오렌지’
• 3 \(\to\) ‘자동차’
• 4 \(\to\) ‘오토바이’

_dct = {0:'사과',1:'배',2:'오렌지',3:'자동차',4:'오토바이'}
lst = list(map(lambda x: _dct[x],x))
lst[:10] # 첫 10개만 출력

['배', '배', '오토바이', '사과', '오렌지', '자동차', '오렌지', '배', '오토바이', '오토바이']

2.

1의 결과에서 아래와 같은 변환을 수행하라.

• ‘사과’ \(\to\) ‘과일’
• ‘배’ \(\to\) ‘과일’
• ‘오렌지’ \(\to\) ‘과일’
• ‘자동차’ \(\to\) ‘탈것’
• ‘오토바이’ \(\to\) ‘탈것’

_dct = {'과일':['사과','배','오렌지'],'탈것':['자동차','오토바이']}
rslt = [key for l in lst for key in _dct if l in _dct[key]]
rslt[:10] # 첫 10개만 출력

['과일', '과일', '탈것', '과일', '과일', '탈것', '과일', '과일', '탈것', '탈것']